All About Diffraction Gratings
Diffraction gratings are optical components critical for a wide variety of applications including spectrometers, other analytical instruments, telecommunications, and laser systems. Gratings contain a microscopic and periodic groove structure - which splits incident light into multiple beam paths through diffraction, causing light of different wavelengths to propagate in different directions. This makes the function of diffraction gratings similar to that of dispersion prisms, although the prism separates wavelengths through wavelength-dependent refraction instead of diffraction (Figure 1). For a discussion of the differences between diffraction and refraction, please visit our Optics 101: Level 1 Theoretical Foundations application note.
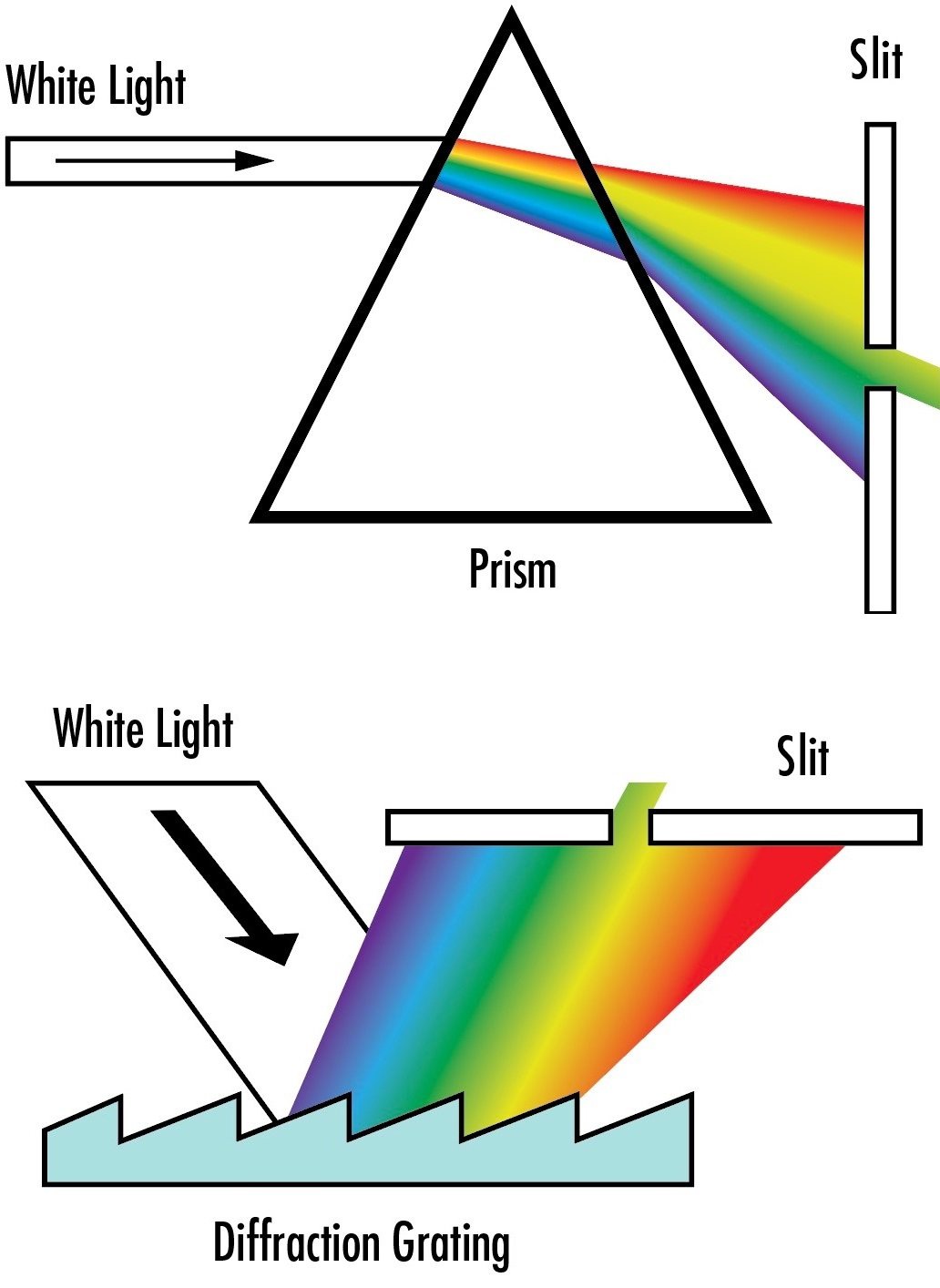
Figure 1: While dispersion prisms separate wavelengths through refraction (top), diffraction gratings instead separate wavelengths through diffraction because of their surface structure (bottom).
Light incident on a grating is diffracted following the grating equation:
m is an integer value describing the diffraction (or spectral) order, λ is the light’s wavelength, d is the spacing between grooves on the grating, α is the incident angle of light, and β is the diffracted angle of light leaving the grating. Constructive interference of different diffractive wavefronts occurs at integer multiples of the wavelength, which is why “m” appears in Equation 1. m defines the diffraction orders, where diffracted angles m = 1 are considered to be “1st order” diffraction, angles where m = 2 are considered to be “2nd order” diffraction, and so on (Figure 2). If m=0, light is either directly reflected off the grating or transmitted through it, depending on if it is a reflection or transmission grating, and this light is considered the “0 order” diffraction. Opposite of dispersion prisms, the lower wavelengths are always closer to the directly reflected or transmitted light, in this case the 0 order. There will be some overlap between different orders. All angles are measured from the grating normal incidence (perpendicular to the grating).
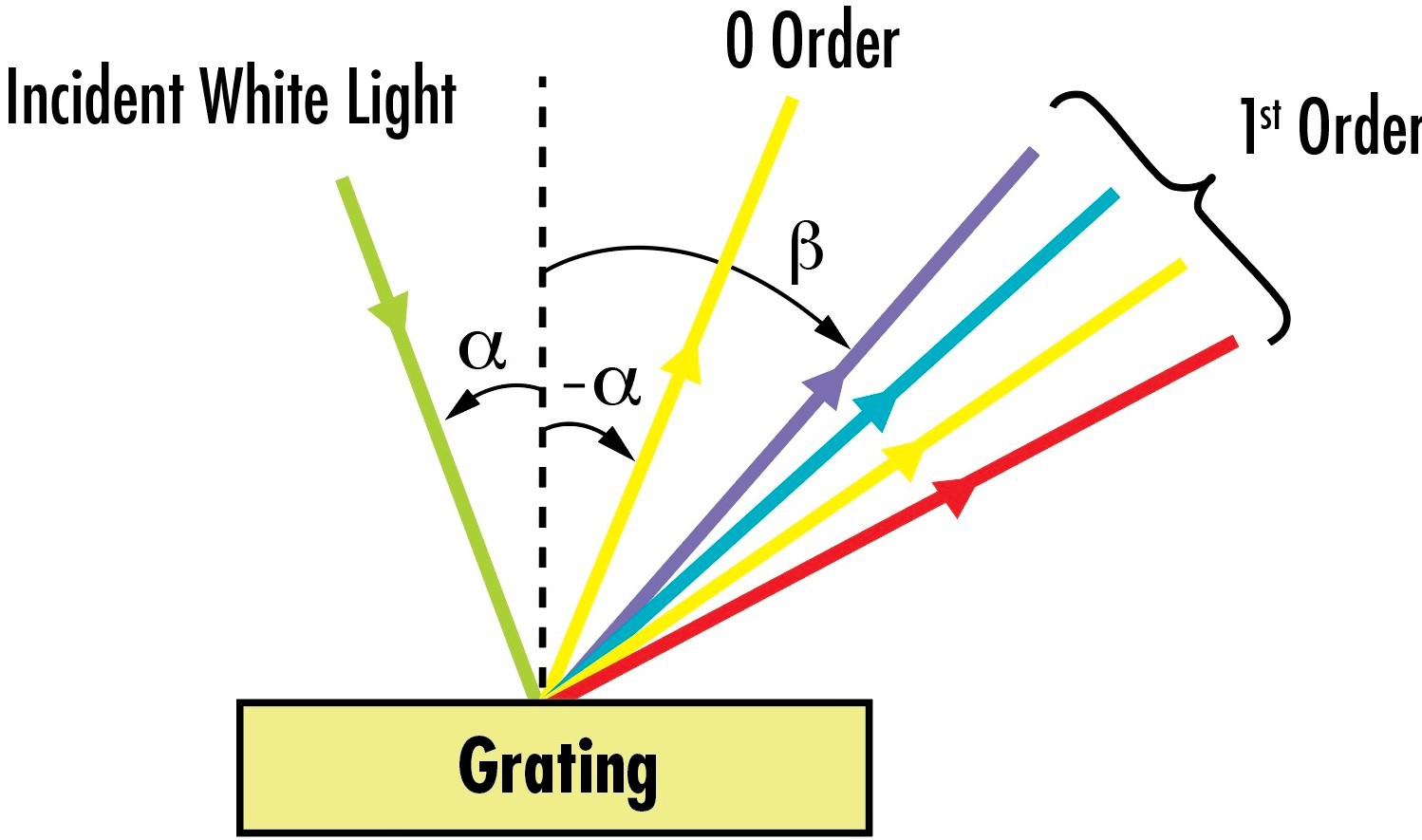
Figure 2: While some light reflects directly off of this grating as “0 order” diffraction, other parts of the incident light are diffracted into 1st order angles based on wavelength. Smaller amounts of the incident light will also be separated into larger 2nd and 3rd orders at higher angles.
A grating’s groove pattern, or the spacing between grooves (d), determines the angles at which different orders are diffracted. In some situations, the groove spacing may be designed to vary across the grating for different levels of diffraction across the part. The grating’s groove profile, on the other hand, describes their shape and determines how much light is diffracted and how much simply reflects off of, or transmits through, the grating. Efficiency charts are used to characterize the percentage of light that will be diffracted at each wavelength. Efficiency will be unique for different polarization states, so efficiency charts usually show different curves for both s- and p-polarization. Metallic or dielectric coatings are often added to gratings to make them reflective and/or increase efficiency.
What Should You Look for When Choosing a Grating?
When choosing a grating it is important to specify the wavelength range, blaze wavelength (which is the wavelength in the diffracted spectrum with the highest efficiency), and blaze angle. The blaze angle describes the first order diffracted angle of the blaze wavelength. At this angle, α and β are equal in Equation 1 and incident light is diffracted back in the exact same direction it came from. This situation is also called the Littrow configuration. Coming close to this angle in a system results in maximum efficiency.
Groove density, or frequency, is typically specified, and this is the inverse of the groove spacing (d). A key property of the optical system is its level of dispersion, but this depends on both the properties of the grating and how it is used. A grating itself cannot be given a specification detailing how a certain amount of rotation corresponds with a certain separation of wavelengths without knowing other system details. A grating’s resolving power may also be specified, which is related to the system’s spectral resolution. However, this resolution depends on both the grating and the system’s entrance and exit slits. The grating’s resolving power (R) is dependent on the spectral order (m) and the number of grooves under illumination (N):
There are often so many grooves under illumination that the entrance and exit slits are the limiting factors for system resolution, not the grating. Efficiency curves may also be useful for verifying the level of diffraction across all wavelengths that will be used in the application.
Gratings should be at least as large as the incident light cone or beam, or else light from the edges will be lost. Therefore, a grating should always be underfilled to prevent stray light from bouncing around the system and creating false signals.
Types of Gratings
Reflection vs. Transmission Gratings
The two broadest categories of diffraction gratings are reflection and transmission gratings. Figures 1 and 2 show reflection gratings, which are essentially mirrors with microscopic grooves. All diffracted orders reflect off of the grating at different angles. Transmission gratings are like lenses with microscopic grooves, and all diffracted orders transmit through the grating but are offset by angles following Equation 1. Reflection gratings are also commonly known as reflective gratings and transmission gratings are also known as transmissive gratings.
Ruled vs. Holographic Gratings
Both reflection and transmission gratings can be further broken down into ruled or holographic gratings, which differ in the way that the groove profile is created. The grooves in ruled gratings are mechanically scribed, or cut, into the part, while the grooves in holographic gratings are optically introduced. In holographic gratings, a light-sensitive material called photoresist is deposited onto the substrate and exposed to an optical interference pattern which interacts with the photoresist. Chemicals are then used to remove remaining photoresist, leaving behind a grating pattern. Ruled gratings typically have triangular grooves, such as those shown in Figure 1, while holographic gratings generally have sinusoidal grooves, (Figures 3 and 4).
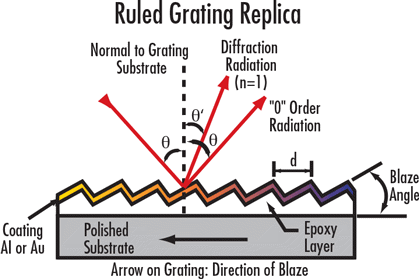
Figure 3: Ruled diffraction gratings typically feature triangular grooves.
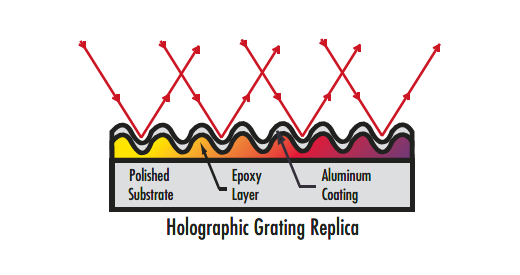
Figure 4: Holographic diffraction gratings typically feature sinusoidal grooves.
Echelle Gratings
Echelle gratings feature a higher groove spacing, or lower groove density, than other gratings, typically by around a factor of 10 but sometimes as high as a factor of 100. Illuminating an Echelle grating at a high angle of incidence (α) will result in high dispersion, resolving power, and efficiency with a low dependence on polarization. These gratings are ideal for situations where high resolution is needed, such as sensitive astronomical instruments and systems striving for atomic resolution.
Plane vs. Concave Gratings
All of the above grating types can again be broken down into plane (or plano-) and concave gratings, which describes their overall shape. Plane gratings are flat and much more common. If their grooves are straight and equally spaced, the grating is flat, and incident light is collimated, all of the diffracted light will be collimated. This is beneficial in many applications because the focal properties of the system are wavelength independent. Plane gratings also generally reduce system complexity compared to concave gratings. Concave gratings are curved and therefore either converge or diverge light. This can be useful for reducing the total number of optical components needed in a system, but the focal properties of the system will be wavelength-dependent.
Grating Applications
Gratings are used in a wide variety of different applications, but common systems include:
Monochromators
Monochromators use concave or plane gratings along with concave mirrors to select a narrow wavelength band out of incident light. If a white light source is incident on one of these devices, they can filter out all wavelengths except for the intended narrow output band. Figure 5 demonstrates how monochromators rotate gratings so that different wavelengths are allowed to pass through an exit slit, while all other wavelengths are blocked.
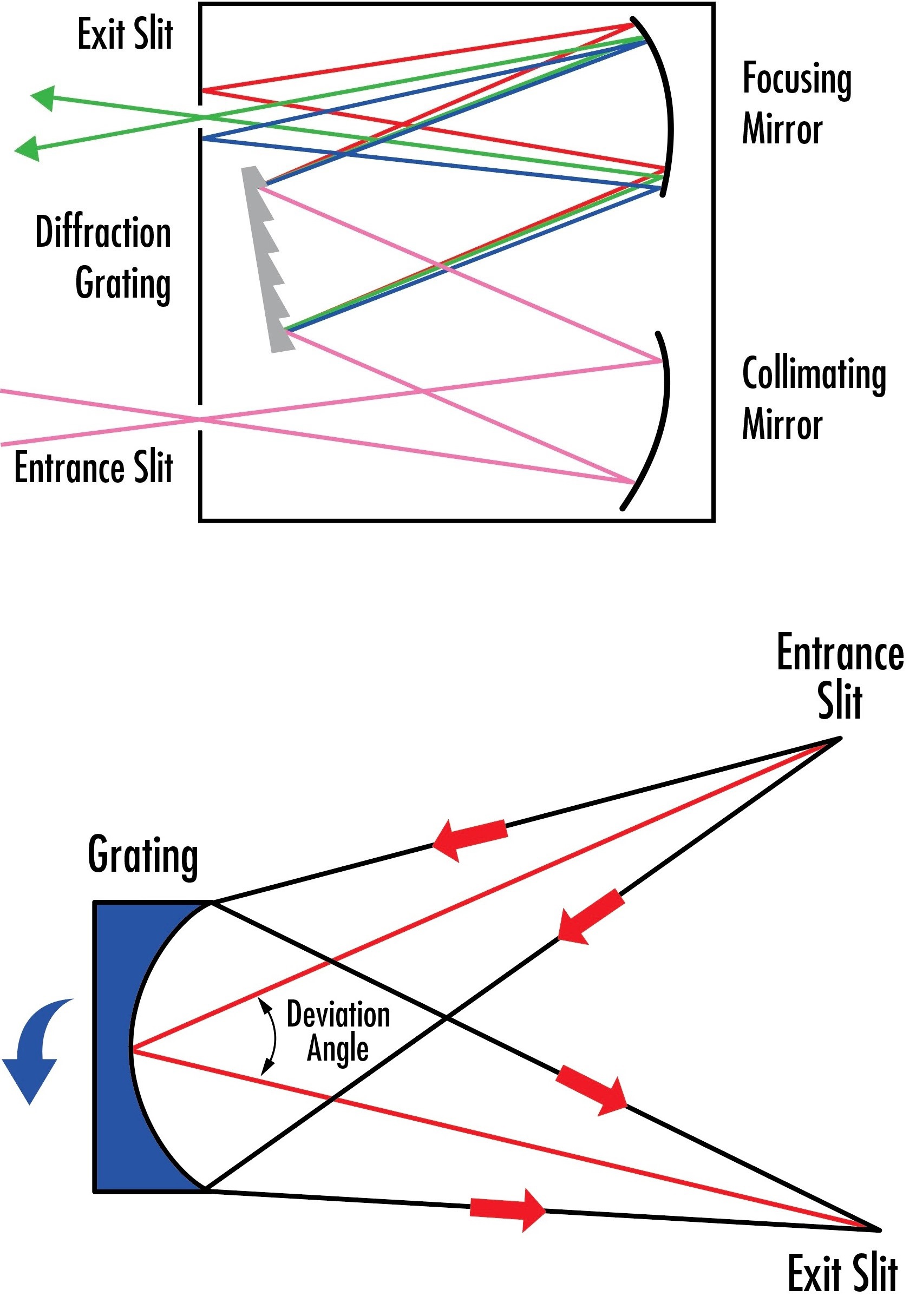
Figure 5: Both plane grating monochromators (top) and concave grating monochromators (bottom) rotate gratings to scan diffracted orders across the exit slit and precisely determine what wavelengths can leave the device.
Spectrographs
Spectrographs split up wavelengths from a broadband light source just like monochromators, but they have no moving parts. Instead, all separated wavelengths are imaged simultaneously on a detector array (Figure 6). Each wavelength is imaged to a different set of pixels, allowing the device to determine the amount of each wavelength present in the broadband source. Spectrographs are often used when a quick analysis of a spectrum is needed, as time is saved by eliminating the need to scan different wavelengths across the detector.
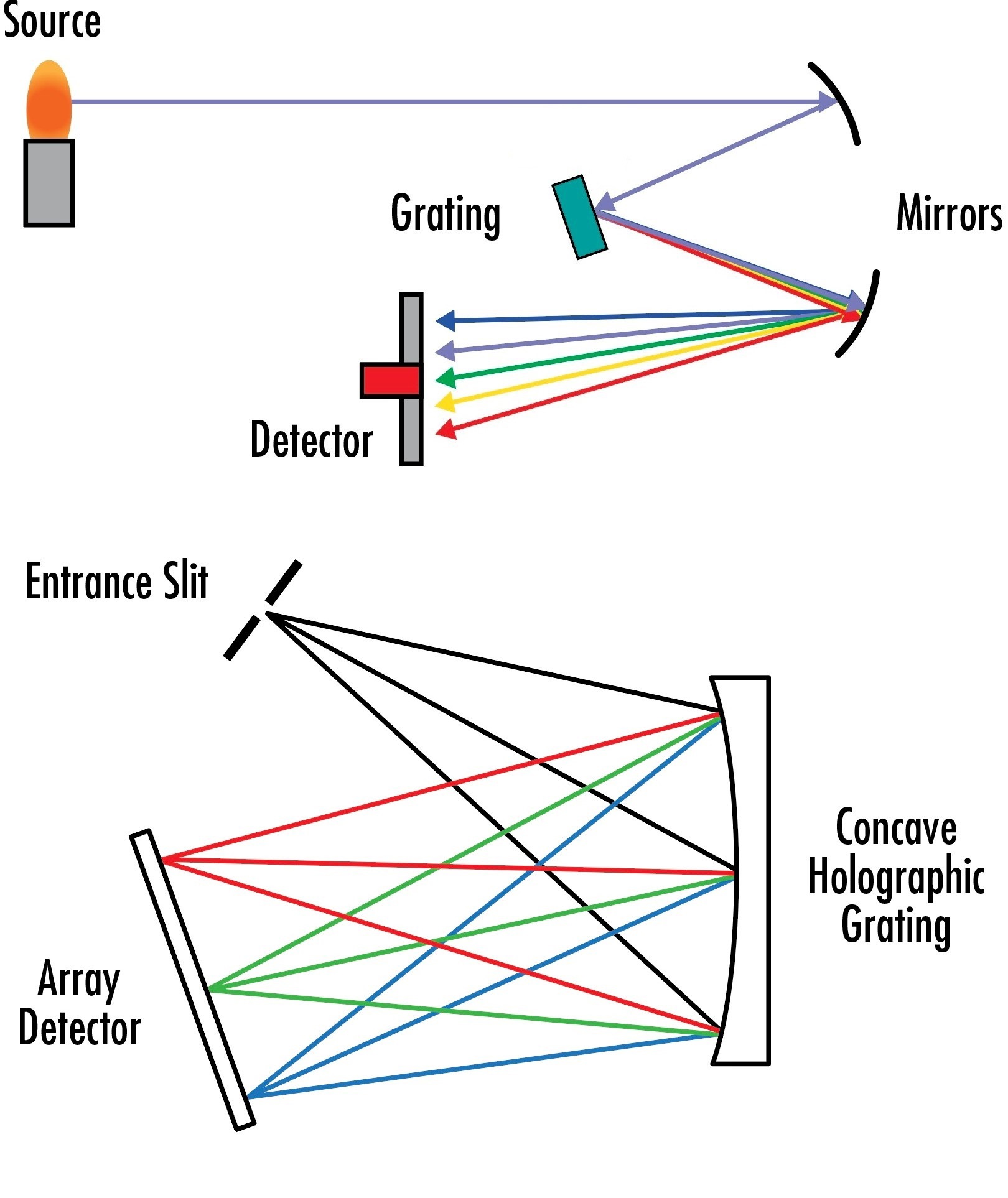
Figure 6: Both plane grating spectrographs (top) and concave grating spectrographs (bottom) use stationary gratings to separate incident wavelengths into different pixels on a detector array.
Laser Tuning
There are several different ways in which diffracting gratings can be used to tune the spectral output of a laser or narrow the output waveband. Gratings can be rotated so that the laser output is only a certain diffracted order, the grating could be stationary as a mirror is rotated to filter the output waveband, and gratings can replace mirrors in a laser to make the output waveband narrower (Figure 7).
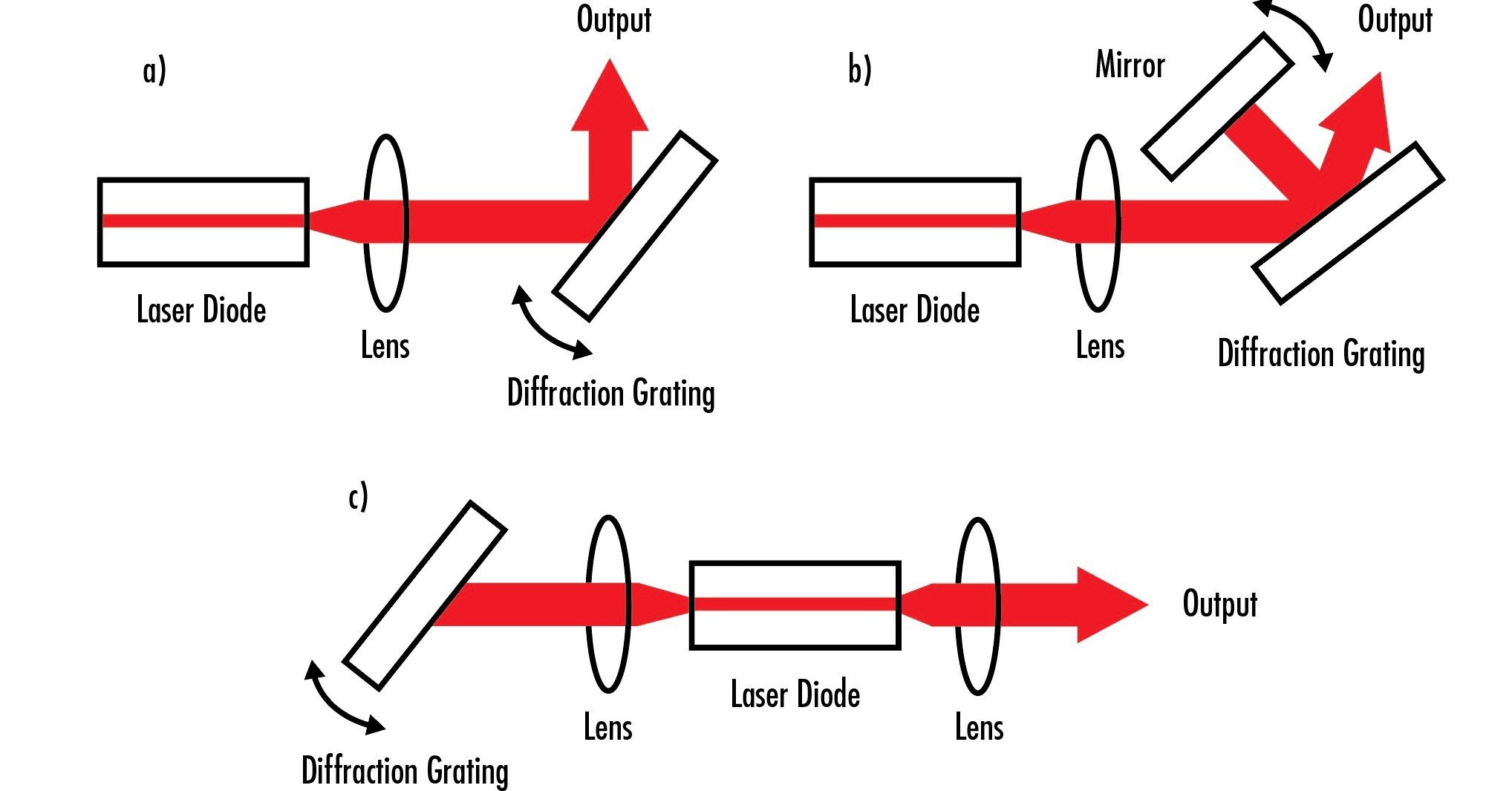
Figure 7: These three setups show the different ways that gratings can be used to tune a laser’s output wavelengths or narrow the output wavelength range.
Laser Pulse Compression, Stretching, and Amplification
Laser pulses with short pulse durations, like those from ultrafast lasers, often have high peak powers that can damage sensitive optical coatings and components. To avoid this, sometimes a pair of diffraction gratings is used to stretch out a pulse, increasing its pulse duration and reducing its peak power. Then this stretched pulse can go through an optical amplifier and have its power increased without damaging any optical components. Another grating pair in the reverse configuration can then compress the pulse duration after the amplifier, resulting in a short, high power pulse at the target (Figure 8).
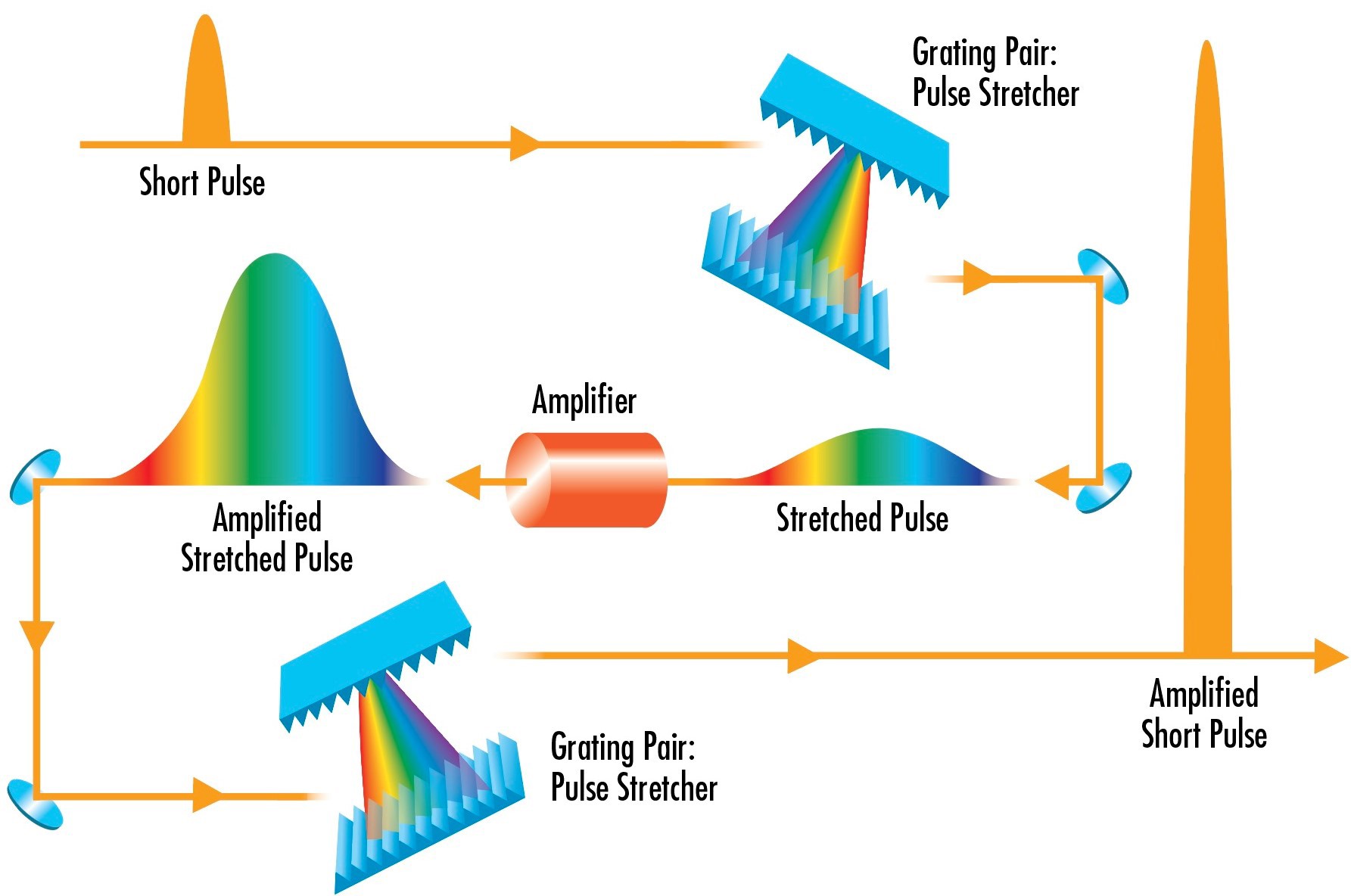
Figure 8: Gratings can be used in pulsed laser systems to both increase pulse duration to prevent laser-induced damage in the system and decrease pulse duration to result in a high-power pulse at the target.
Gratings from Edmund Optics®
Edmund Optics® offers a wide range of diffraction gratings spanning the entire range of options discussed above.
Ruled Reflective Diffraction Gratings

- Superior Efficiency at Design Wavelength Compared with Holographic Gratings
Holographic Reflective Diffraction Gratings

- Reduced Stray Light While Maintaining High Diffraction Efficiency
Echelle Reflective Gratings

- Highest Resolving Power and Dispersion from NUV to IR
Concave Diffraction Gratings

- Function as Focusing and Dispersing Element and Therefore Reduce Number of Optics Required in Spectrometers While Showing Low Aberrations
Transmissive Diffraction Gratings

- Separate (Diffract) Polychromatic Light into its Component Wavelengths by Transmission
Polarization Gratings

- Selectively Diffract Light Based on Polarization
More Resources
- FAQ: What is the grating equation?
- FAQ: What is the difference between reflective and transmission gratings?
- FAQ: What is the difference between holographic and ruled diffraction gratings?
- FAQ: How do the efficiency curves relate to the actual amount of light I will see at any given wavelength?
- FAQ: What is the blaze angle and blaze wavelength of a grating and how are they related?
- FAQ: What is stray light and how will it affect my system?
- FAQ: How do I handle and clean my gratings?
- FAQ: What is the difference between Rowland circle and polychromator mounts for gratings?



























or view regional numbers
QUOTE TOOL
enter stock numbers to begin
Copyright 2023, Edmund Optics Inc., 14F., No.83, Sec. 4, Wenxin Road, Beitun District , Taichung City 406, Taiwan (R.O.C.)
California Consumer Privacy Act (CCPA): Do Not Sell My Information